Programming the Shor's Algorithm to Crack the RSA Cryptography

In the previous post, we showed Shor’s Algorithm, the theory behind cracking of the RSA using Quantum Computing. In this post, we will show how to program the algorithm using QISKit in order to appreciate how the theory is implemented.

Brief Review of RSA Cryptography

According to the RSA encryption, we choose 2 prime numbers $p$ and $q$ and form a product $N=pq$. Then we choose a number $e$ that has no common factor with $p-1$ and $q-1$. The set of numbers $N$ and $e$ is the public key.

If we have a message $m$, then the encrypted message (or ciphertext) is computed using the formula.

\[c = m^e \mod N\]

The public only knows about $N$, $e$ and $c$. What we want to do is to decrypt the message $c$ using Quantum Computing by a process known as period finding. The period $r$ is an integer defined by

\[c^r \mod N = 1\]

Once $r$ is found, we can compute $d^\prime$ satisfying

\[ed^\prime \mod r = 1\]

From there, we can finally decrypt our message

\[c^{d^\prime} \mod N = (m^{e})^{d^\prime} = m^{ed^\prime} = m^{s\cdot r + 1}\]

Since $r$ is the period:

\[c^{d^\prime} \mod N = m\cdot (m^r)^s = m(1)^s = m \mod N\]

Example

Let $p=3$ and $q=5$. Let $e=3$ since it has not common factors with $p-1=2$ and $q-1=4$. If our message is $m=7$, then the encrypted message is

\[\begin{array}{rl} c&=m^3 \mod N \\ &= 7^3 \mod 15\\ &= 13 \end{array}\]

Given only the knowledge of $c=13$, $e=3$ and $N=15$, we want to find the original message $m$.

Overview of Shor's Algorithm

We will setup two registers for the Shor’s Algorithm. The first register is the input register. These are the qubits whose value we will input into the modular exponentiation function. The output of that function will be stored in the output register.

The modular exponentiation function is defined as:

\[f(x) = c^x \mod N\]

Shor’s algorithm involves:

Generating a superposition of all numbers $x$ from 0 to $2^n-1$ and computing the modular exponentiation of the the numbers modulo $N$.

\[\displaystyle \frac{1}{\sqrt{2^n}}\sum_{x=0}^{2^n-1} |x\rangle|c^x \mod N\rangle\]

We then measure the output register. This will give us a value say $f(x_0)$. In the process of measurement, this will collapse the state of the input register into

\[|\psi\rangle = \displaystyle \frac{1}{\sqrt{m}}\sum_{k=0}^{m-1} |x_0 + kr\rangle\]

Next, we apply the Fourier Transform to the input register. The Fourier Transform is defined in the computational basis is:

\[\mathbf{U}_{\mathrm{FT}}|x\rangle = \displaystyle \frac{1}{\sqrt{2^n}} e^{2\pi i xy/2^n}|y\rangle\]

So applying this to the input register will give:

\[\begin{array}{rl} \displaystyle \mathbf{U}_{\mathrm{FT}}\frac{1}{\sqrt{m}}\sum_{k=0}^{m-1} |x_0+kr\rangle &= \displaystyle \frac{1}{\sqrt{m}}\sum_{k=0}^{m-1} \mathbf{U}_\mathrm{FT}|x_0+kr\rangle\\ &= \displaystyle \sum_{y=0}^{2^n-1} \underbrace{e^{2\pi i x_0y/2^n}\frac{1}{\sqrt{2^nm}}\sum_{k=0}^{m-1} e^{2\pi ikry/2^n}}_{\text{probability amplitude}}|y\rangle \end{array}\]

In other words, the input register will become a superposition of states whose probability of occurring is given by the square of the probability amplitude above.

We then measure the input register to get a value $\vert y\rangle$.
Compute the period using the continued fraction expansion of

\[\displaystyle \frac{y}{2^n}\]

The fraction $\displaystyle \frac{j}{r}$ (for some integer j) will appear as one of the partial sums of the continued fraction expansion.

Verify that the computed period is indeed a period by satisfying

\[c^r \mod 15 = 1\]

Compute $d^\prime$, the inverse modulo of $e$ using the formula:

\[ed^\prime = s\cdot r + 1\]

where $s$ is an integer.

Use the computed $d^\prime $ to compute the message from the ciphertext:

\[m = c^{d^\prime}\]

Implementation Using QISKit

There are two important circuits we need to create in order to implement Shor’s algorithm. The first is the modular exponentiation and the second is the Fourier Transform. For the modular exponentiation, we are going to implement a similar function that will give the answer specifically to our problem.

The ciphertext we are trying to decrypt is $c=13 \mod 15$. Below is a table of result for the modular exponentiation. In the binary representation, the most significant bit is to the left.

\[\begin{array}{|c|c|c|c|}\hline x & x\text{ in binary } & f(x) = 13^n \mod 15 & f(x) \text{ in binary}\\\hline 0 & 0000 & 1 & 0001\\ 1 & 0001 & 13 & 1101\\ 2 & 0010 & 4 & 0100\\ 3 & 0011 & 7 & 0111\\ 4 & 0100 & 1 & 0001\\ 5 & 0101 & 13 & 1101 \\ 6 & 0110 & 4 & 0100\\ 7 & 0111 & 7 & 0111\\ 8 & 1000 & 1 & 0001\\ 9 & 1001 & 13 & 1101\\ 10 & 1010 & 4 & 0100\\ 11 & 1011 & 7 & 0111\\ 12 & 1100 & 1 & 0001\\ 13 & 1101 & 13 & 1101\\ 14 & 1110 & 4 & 0100\\ 15 & 1111 & 7 & 0111\\\hline \end{array}\]

If you study the table above, you will notice that for numbers ending in the following suffixes, following mappings are true:

\[\begin{array}{rl} 00 &\rightarrow 0001\\ 01 &\rightarrow 1101\\ 10 &\rightarrow 0100\\ 11 &\rightarrow 0111 \end{array}\]

Here is a circuit to implement this mapping:

To verify this, if the input is ends with 00, the output register $qout_0$ will flip to 1 because of the NOT gate $X$. When the input ends in “01”, the two Controlled-NOTs at $qin_0$ will flip the bits $qout_2$ and $qout_3$. When the input ends in “10”, the two Controlled-NOTs in $qin_2$ will flip the bits at $qout_0$ and $qout_2$. Finally, when the input ends in “11”, all gates starting from the left will be applied. The net result will be that $qout_0,qout_1$ and $qout_2$ will be set to 1 while $qout_3$ will be set to 0.

The QISKit code to implement this is:

input_register  = QuantumRegister(4,name="qin")
output_register = QuantumRegister(4,name="qout")

c  = ClassicalRegister(8)
qc = QuantumCircuit(input_register, output_register)
qc.barrier()

qc.x(output_register[0])
qc.barrier()

qc.cx(input_register[0],output_register[2])
qc.cx(input_register[0],output_register[3])
qc.barrier()

qc.cx(input_register[1],output_register[2])
qc.cx(input_register[1],output_register[0])
qc.barrier()

qc.ccx(input_register[0],input_register[1],output_register[3])
qc.ccx(input_register[0],input_register[1],output_register[2])
qc.ccx(input_register[0],input_register[1],output_register[1])
qc.ccx(input_register[0],input_register[1],output_register[0])
qc.barrier()

qc.draw(output='mpl')

Implementing the Fourier Transform

We will use the Fourier Transform circuit derived in this blog post. Here are the sequence of gate operations to implement the Fourier Transform:

\[\mathbf{U}_{FT}|x_3\rangle|x_2\rangle|x_1\rangle|x_0\rangle = \displaystyle \mathbf{H}_3\mathbf{V}_{23}\mathbf{H}_2\mathbf{V}_{13}\mathbf{V}_{12}\mathbf{H}_1\mathbf{V}_{03}\mathbf{V}_{02}\mathbf{V}_{01}\mathbf{H}_0|x_0\rangle|x_1\rangle|x_2\rangle|x_3\rangle\]

where $\mathbf{V}_{ij}$ is the controlled-phase rotation gate defined by

\[\begin{array}{rl} \mathbf{V}_{ij}|x_{n-1}\cdots x_j\cdots x_i\cdots 0\rangle &= e^{\pi i x_ix_j/2^{|i-j|}}|x_{n-1}\cdots x_j\cdots x_i\cdots 0\rangle \end{array}\]

Using QISKit, we can visualize the circuit using the code below:

input_register  = QuantumRegister(4,name="qin")
output_register = QuantumRegister(4,name="qout")
c               = ClassicalRegister(4)

qc = QuantumCircuit(input_register,c)
qc.h(input_register[0])
qc.cu1(math.pi/float(2),input_register[0],input_register[1])
qc.cu1(math.pi/float(2**2),input_register[0],input_register[2])
qc.cu1(math.pi/float(2**3),input_register[0],input_register[3])
qc.barrier()

qc.h(input_register[1])
qc.cu1(math.pi/float(2),input_register[1],input_register[2])
qc.cu1(math.pi/float(2**2),input_register[1],input_register[3])
qc.barrier()

qc.h(input_register[2])
qc.cu1(math.pi/float(2),input_register[2],input_register[3])
qc.h(input_register[3])
qc.barrier()

The Complete Shor's Algorithm Circuit

Now that we have created the circuits for the “modular exponentiation” and the Fourier Transform, we will combine them to create the circuit for the period finding algorithm.

Here’s the complete code:

from qiskit import Aer

import math

from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister, execute
from qiskit.tools.visualization import circuit_drawer, plot_histogram
from qiskit import BasicAer

backend = BasicAer.get_backend('qasm_simulator')

input_register  = QuantumRegister(4)
output_register = QuantumRegister(4)
c = ClassicalRegister(8)

qc = QuantumCircuit(input_register, output_register,c)
qc.h(input_register)
qc.barrier()

qc.x(output_register[0])
qc.barrier()

qc.cx(input_register[0],output_register[2])
qc.cx(input_register[0],output_register[3])
qc.barrier()

qc.cx(input_register[1],output_register[2])
qc.cx(input_register[1],output_register[0])
qc.barrier()

qc.ccx(input_register[0],input_register[1],output_register[3])
qc.ccx(input_register[0],input_register[1],output_register[2])
qc.ccx(input_register[0],input_register[1],output_register[1])
qc.ccx(input_register[0],input_register[1],output_register[0])
qc.barrier()

# measure the output
qc.measure([4,5,6,7],[4,5,6,7])
qc.barrier()


#Apply the Fourier Transform to the new state of the input register.
qc.h(input_register[0])
qc.cu1(math.pi/float(2),input_register[0],input_register[1])
qc.cu1(math.pi/float(2**2),input_register[0],input_register[2])
qc.cu1(math.pi/float(2**3),input_register[0],input_register[3])
qc.barrier()

qc.h(input_register[1])
qc.cu1(math.pi/float(2),input_register[1],input_register[2])
qc.cu1(math.pi/float(2**2),input_register[1],input_register[3])
qc.barrier()

qc.h(input_register[2])
qc.cu1(math.pi/float(2),input_register[2],input_register[3])
qc.h(input_register[3])
qc.barrier()

qc.measure([0,1,2,3],[0,1,2,3])

qc.draw(output='mpl')

We then execute this code 1000 times in order to get the probability distributions.

job = execute(qc, backend,shots=1000)
result=job.result()
counts= result.get_counts(qc)
print(counts)
plot_histogram(data=counts, figsize=(14,10))

Interpreting the Result

The count of the resulting states can be printed using

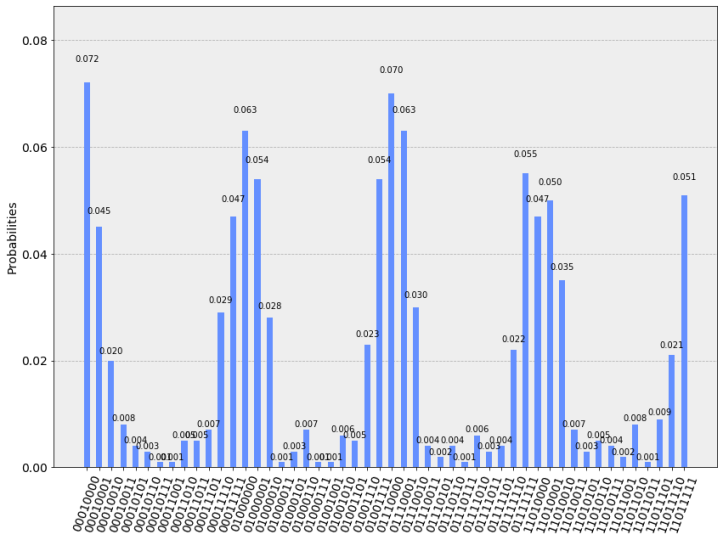
print(counts)

In one of the runs, this is the result we got:

{'01111010': 7, '11010000': 66, '11010011': 7, '00010111': 3, '01000010': 35, '11010110': 1, '11011011': 5, '11010001': 30, '01110101': 1, '01111101': 6, '01110111': 2, '01000001': 42, '11010101': 2, '11011001': 1, '00010011': 7, '11011101': 9, '01001110': 23, '01001111': 63, '01110011': 9, '00011111': 55, '00011110': 22, '00010000': 61, '11010111': 3, '01110000': 57, '01110001': 55, '01110010': 28, '01000110': 4, '00010010': 18, '00010001': 56, '00010101': 3, '00011001': 4, '00011010': 5, '11011110': 35, '00010110': 5, '01001010': 6, '00011101': 8, '11011010': 1, '01001001': 2, '11010010': 26, '01111111': 55, '00011011': 4, '01000101': 3, '01001011': 4, '01000011': 6, '01000000': 60, '01001101': 2, '01111110': 25, '11011111': 57, '01111001': 4, '01110110': 7}

The important qubits to look at are the input qubits. Remember that the qubits are represented from the right to left. So the input qubits are the 4 qubits at the right-most, where the first input qubit is the right-most qubit. For example, in the result 01111101, the input qubits are the 4 qubits at the right-most:

\[01111101 \equiv \underbrace{0111}_{\text{output}}\underbrace{1101}_{\text{input}}\]

For this result, the input qubits are 1101. However, because of the design of the Fourier Transform, the order of the qubits are actually reversed and should be 1011, which correspond to the decimal number 11.

Here is a python script shor_expt.py that will make the output easier to read. It will output the count, together with the reversed order of the qubits and the decimal equivalent:

x={'01111010': 7, '11010000': 66, '11010011': 7, '00010111': 3, '01000010': 35, '11010110': 1, '11011011': 5, '11010001': 30, '01110101': 1, '01111101': 6, '01110111': 2, '01000001': 42, '11010101': 2, '11011001': 1, '00010011': 7, '11011101': 9, '01001110': 23, '01001111': 63, '01110011': 9, '00011111': 55, '00011110': 22, '00010000': 61, '11010111': 3, '01110000': 57, '01110001': 55, '01110010': 28, '01000110': 4, '00010010': 18, '00010001': 56, '00010101': 3, '00011001': 4, '00011010': 5, '11011110': 35, '00010110': 5, '01001010': 6, '00011101': 8, '11011010': 1, '01001001': 2, '11010010': 26, '01111111': 55, '00011011': 4, '01000101': 3, '01001011': 4, '01000011': 6, '01000000': 60, '01001101': 2, '01111110': 25, '11011111': 57, '01111001': 4, '01110110': 7}


for k in x.keys():
  h=k[4:]
  hrev = h[::-1]
  sum = 0
  for i in range(0,4):
    sum += pow(2,3-i)*int(hrev[i])

  print("%s %s %s %2d %2d" % ( k, h, hrev, sum, x[k]))

Running this script and sorting the result, we get:

$ python shor_expt.py|sort -r -k 5

11010000 0000 0000  0 66
01001111 1111 1111 15 63
00010000 0000 0000  0 61
01000000 0000 0000  0 60
11011111 1111 1111 15 57
01110000 0000 0000  0 57
00010001 0001 1000  8 56
01111111 1111 1111 15 55
01110001 0001 1000  8 55
00011111 1111 1111 15 55
01000001 0001 1000  8 42

The last column is the count and the column before that is the number $y$ which we will use later to compute for the period. We can see that the numbers 0, 15 and 8 occur with very high frequency. We can ignore zero as it will not give us the period. We can use 15 or 8.

Computing the Period

Now that we have a $y$, we can use continued fraction expansion to compute for the period, which is a partial sum of the expansion. If we choose $y=15$, we have

\[\begin{array}{rl} \displaystyle \frac{y}{2^n} &= \displaystyle \frac{15}{2^4} \\[10px] &= \displaystyle \frac{15}{16}\\[10px] &= \displaystyle \frac{1}{1+\displaystyle \frac{1}{15}} \end{array}\]

which terminates. So the partial sum is also $\displaystyle \frac{15}{16}$ and the period is 16. Verifying if it’s a period, we have

\[13^{16}\mod 15 = 1\]

which is indeed a period.

We then compute the inverse modulo using the formula

\[ed^\prime = s\cdot r + 1 \Longrightarrow 3d^\prime = s\cdot 16 + 1\]

which will be satisfied if s=5 and $d^\prime=27$. Finally, using $d^\prime = 27$ we can compute the message $m$:

\[\begin{array}{rl} m &=c^{d^\prime} \mod 15 \\ &= 13^{27}\mod 15\\ &= 7 \end{array}\]

which is our original message!

You can verify that if we use $y=8$, then the period is $r=2$. The correspoding $d^\prime = 3$. Using this value, the message is

\[\begin{array}{rl} m &=c^{d^\prime} \mod 15 \\ &= 13^{3}\mod 15\\ &= 7 \end{array}\]

which gives us the same value.

This completes our implementation of the Shor’s algorithm using QISKit. By implementing the modular exponentiation function as a mapping, we were able to do away with the complexities of a generic modular exponentiation function that will work for any $c$. This allowed us to focus on how the Shor’s algorithm actually works to decrypt the message encoded using RSA.

Image Credit: “WW2 Encryption: Enigma German Machine - cover off” by Whiskeygonebad is marked with CC BY-NC-SA 2.0. To view the terms, visit https://creativecommons.org/licenses/by-nc-sa/2.0/?ref=openverse