Let $y^2 = x^3 + ax + b$ be the equation of the elliptic curve E. Any line L that intersects the curve will intersect the curve in at most 3 points. Below are examples of how these look like.

A mathematical structure can defined on E. We can “add” two points on E to get a third point. First, let’s define the negative of a point. A point $Q$ is the negative of a point $P$ if the point $Q$ is the mirror image of the point $P$ with respect to the x-axis that is,

\[Q = - P\]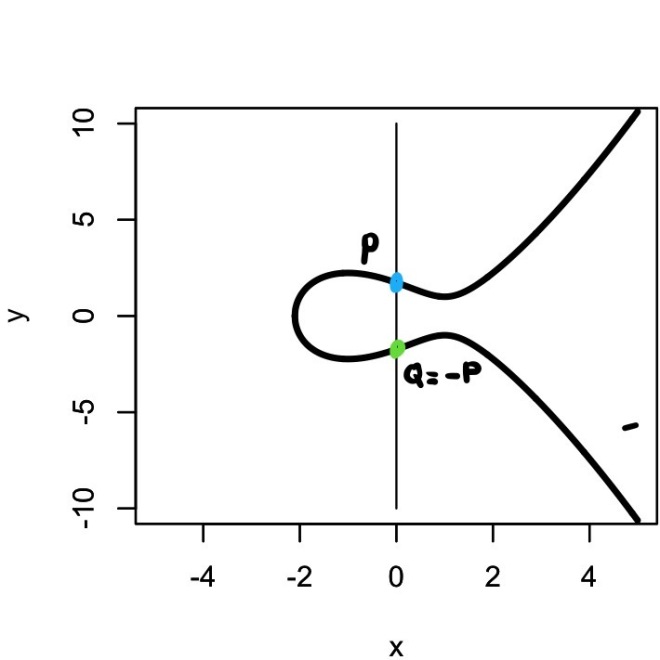

From the relation above, we can define $O$ to be

$$ P + (-P) = O $

The point $O$ is the “point at infinity”.

Let L be a line that intersects E at points $P$, $Q$ and $R$. We define the sum

\[P + Q + R = O\]

From this definition, we see that the the sum of any of the two points is the negative of the third point, that is, $P + Q = -R$.

So how do we actually add 2 points given their coordinates? It turns out that if we are given the x and y coordinates of 2 points, we can easily compute the third point. To see this, let $y = mx +c$ be the equation of the line that intersects the elliptic curve $y^2 = x^3 + ax + b$ at points $P$, $Q$ and $R$. Solving for the x-coordinates of the intersection, we get

\[\begin{array}{rl} \displaystyle x_1 &= \displaystyle \frac{m^2}{3} + \frac{2^{1/3}}{3} A - \frac{B}{3}\\ \displaystyle x_2 &= \displaystyle \frac{m^2}{3} - \frac{(1+i\sqrt{3})}{3 2^{2/3}}A + (1-i\sqrt{3})\frac{B}{6}\\ \displaystyle x_3 &= \displaystyle \frac{m^2}{3} - \frac{(1-i\sqrt{3})}{3 2^{2/3}}A + (1+i\sqrt{3})\frac{B}{6} \end{array}\]

where

\[A = \frac{\left(3 a-6 c m-m^4\right)}{ \sqrt[3]{\sqrt{\left(9 a m^2+27 b-27 c^2-18 c m^3-2 m^6\right)^2+4 \left(3 a-6 c m-m^4\right)^3}+9 a m^2+27 b-27 c^2-18 c m^3-2 m^6}}\] \[B = \frac{\sqrt[3]{\sqrt{\left(9am^2+27b-27c^2-18cm^3-2m^6\right)^2+4\left(3a-6 cm-m^4\right)^3}+9am^2+27b-27c^2-18cm^3-2m^6}}{ \sqrt[3]{2}}\]

From this we see that

\[x_1 + x_2 + x_3 = m^2\]

Therefore, if we have $x_1$ and $x_2$, we can get $x_3$ from the formula:

\[x_3 = m^2 -x_1 -x_2\]

Once we get $x_3$, we can get $y_3$ from the formula of the slope:

\[\begin{array}{rl} \displaystyle \frac{y_3-y_1}{x_3-x_1} &= m\\ y_3-y_1 &= m(x_3 - x_1)\\ y_3 &= m(x_3 - x_1) + y_1 \end{array}\]

The variable $m$ is the slope of the line. If the line is tangent to the curve E at point $P$, the slope $m$ is calculated using the derivative of E at the $P$:

\[\begin{array}{rl} d(y^2) &= d(x^3 + ax + b) \\ 2y dy &= (3x^2 + a) dx\\ \displaystyle \frac{dy}{dx} &= m = \displaystyle \frac{3x^2 +a}{2y} \end{array}\]

Addition Formula

Now that we have seen how to add two points, let’s summarize the formula here:

Given points $P=(x_1,y_1)$ and $Q=(x_2,y_2)$, the third point $R=(x_3, -y_3)$ can be computed from

\[x_3 = m^2 -x_1 -x_2\] \[y_3 = m(x_3 - x_1) + y_1\]

where

\[m = \begin{cases} \displaystyle \frac{y_1 - y_2}{x_1 - x_2} & P \ne Q\\ \displaystyle \frac{3x^2 +a}{2y} & P = Q \end{cases}\]

Important! Take note that $R=(x_3,-y_3)$. The value of $y_3$ should be the negative of the computed value.

Example 1

Let the elliptic curve be $y^2 = x^3 -3 + 3$, then points $P=(-2,1)$ and $Q=(0, 1.732051)$ lie on the curve. The third point can be computed as follows:

\[\begin{array}{rl} m &= \displaystyle \frac{y_1 - y_2}{x_1 - x_2}\\ &= \displaystyle \frac{1-1.732051}{-2 - 0}\\ &= 0.3660255 \end{array}\] \[\begin{array}{rl} x_3 &= m^2 - x_1 - x_2\\ &= (0.3660255)^2 - (-2) - 0\\ &= 2.133975 \end{array}\] \[\begin{array}{rl} y_3 &= m(x_3 - x_1) + y_1\\ &= 0.3660255 ( 2.133975 - (-2)) + 1\\ &= 2.51314 \end{array}\]

Therefore $R=(x_3,-y_3) = (2.133975, -2.51314)$.

Example 2

If $P=Q=(-2,1)$, we have:

\[\begin{array}{rl} m &= \displaystyle \frac{3x^2 +a}{2y}\\ &= \displaystyle \frac{3(-2)^2 -3}{2(1)}\\ &= 4.5 \end{array}\] \[\begin{array}{rl} x_3 &= m^2 - x_1 - x_2\\ &= (4.5)^2 - (-2) - (-2)\\ &= 24.25 \end{array}\] \[\begin{array}{rl} y_3 &= m(x_3 - x_1) + y_1 \\ &= 4.5 ( 24.25 - (-2)) + 1\\ &= 119.125 \end{array}\]

Therefore, $R=(x_3,-y_3) = (24.5, -119.125)$

Group Structure

The set of points of E together with the point at infinity, $E\cup {O}$, forms a group under the addition operation defined above.

• It is associative: $(P+Q) + R = P + (Q+R)$
• Every element has an inverse: $P + (-P) = O$
• It contains the identity element. From the inverse we have $P - P = 0$. Therefore, $P + O = P$, which makes $O$ the identity element.
• It is closed: For every $P, Q$, $P + Q \in E\cup \{O\}$

Modulo Arithmetic

The addition formula also works for modular arithmetic. Let $p$ be a prime number, then given two points $P$ and $Q$, the third point can be computed as

\[x_3 = m^2 -x_1 -x_2 \mod p\] \[y_3 = m(x_3 - x_1) + y_1 \mod p\]

where

\[m = \begin{cases} \displaystyle \frac{y_1 - y_2}{x_1 - x_2} \mod p & P \ne Q\\ \displaystyle \frac{3x^2 +a}{2y} \mod p & P = Q \end{cases}\]

Example

Suppose $p=71$, $P =(0,28)$ and $Q = (-2, 1)$, then we compute the third point $R$ as follows:

\[\begin{array}{rl} m &= \displaystyle \frac{y_1 - y_2}{x_1 - x_2} \mod 71\\ &= \displaystyle \frac{28-1}{0 - (-2)} \mod 71\\ &= 27(36) \mod 71, \text{ where 36 is the inverse of 2 modulo 71}\\ &= 49 \end{array}\] \[\begin{array}{rl} x_3 &= m^2 - x_1 - x_2 \mod 71\\ &= 49^2 - 0 - (-2) \mod 71\\ &= 60 \end{array}\] \[\begin{array}{rl} y_3 &= m(x_3 - x_1) + y_1 \mod 71\\ &= 49(60 - 0) + 28\\ &= 57 \end{array}\]

Therefore, $P+Q = R = (x_3,-y_3) = (60, -57) \mod 71 = (60, 14)$

N-fold Point Addition

Let $B$ be a point in E. If $n$ is an integer greater than 1, the point $nB$ is defined as

\[nB = \underbrace{B + B + \ldots + B}_{\text{n times}}\]

Example

Let $y^2 = x^3 - 3x + 3 \mod 71 $. Let $B=(0,28)$, then using the formula for $x_3$ and $y_3$:

\[\begin{array}{rl} 3B &= (0,28) + (0,28) + (0,28) \mod 71\\ &= (37,63) \mod 71 \end{array}\]

Elliptic Curve Cryptography

Alice and Bob want to exchange information using Elliptic Curve Cryptography. They agree on an elliptic curve equation and a base point $B$. Alice and Bob both choose a random number between 1 and 71. Let $e_a$ and $e_b$ be the secret numbers chosen by Alice and Bob (respectively) and publishes the public keys $e_aB$ and $e_bB$. Alice wants to send the message encoded in a point $P$. She multiplies Bob’s public key and her private key and adds it to the message $P$ to get $P+ e_ae_bB$ and sends the pair ${e_aB, P + e_ae_bB}$.

Bob receives the message multiplies his private key to Alice’s public key to get $e_be_aB$. He then subtracts this to the message $P+ e_ae_bB$ to get the original message $P$.

Assume Bob and Alice agree on the equation $y^2 = x^3 - 3x + 3$, the base point $B=(0,28)$ and the modulus p=71. Suppose Alice’s private key is 4 and Bob’s private key is 5. Alice will publish her public key as $e_aB = 4B = (42,57)$. Likewise, Bob will publish his public key as $e_bB = 5B=(30,2) $.

Alice wants to send Bob a message encoded in the point $P=c(2,17)$ of E. First, Alice will multiply Bob’s public key with her private key to get $e_ae_bB = 4\cdot (30,2) = (18,32)$. She will then add this to $P$ to get encrypted message $P + e_ae_bB = (2,17) + (18,32) = (10,11)$. She will send $(10,11)$ to Bob.

Bob then receives the message $(10,11)$. The first thing he will do is to multiply Alice’s public key $e_aB = (42,57)$ with his private key to get $e_be_aB = 5\cdot(42,57) = (18,32)$. Next, he will subtract this from the encrypted message to get $(10,11) + (18,-32) = (2,17)$, which is the unencrypted message of Alice!

Image Used: “Elliptic Curve inside the missile silo at ToorCamp 2009” by caseorganic is marked with CC BY-NC 2.0. To view the terms, visit https://creativecommons.org/licenses/by-nc/2.0/?ref=openverse